编者荐语
本次推荐的是我院胡安宁教授发于《社会学研究》上的文章《处理效应异质性分析——机器学习方法带来的机遇与挑战》
原文刊发于《社会学研究》2021年第1期,原文链接:http://shxyj.ajcass.org/Magazine/Show?id=76588
摘要
处理效应异质性是定量社会科学关注的重点。本文以因果随机森林与贝叶斯叠加回归树为例,指出以算法为导向的新兴分析手段可以克服模型形式和变量选择的限制,并考虑变量间各种交互关系。因果随机森林与贝叶斯叠加回归树分别体现了“匹配”和“模拟”的分析逻辑,以帮助研究者勾勒出异质性处理效应的经验分布并探索该异质性的决定因素。然而,参数设定差异和算法差异都会损害处理效应异质性分析结果的稳健性。
一、问题的提出
社会科学经验研究往往围绕变量之间的关系展开。随着因果推论方法在社会科学领域内的逐渐普及,定量社会科学研究逐渐从强调相关关系转向强调因果关系(胡安宁,2012;Morgan & Winship,2015)。除了常规的平均因果效应之外,越来越多的学者开始关注处理效应的异质性(谢宇,2008)。这种对于异质性的考察有其社会学基础。一方面,大量的社会学中层理论都是围绕特定人群的细分展开的,凸显了个体间的异质性。这也就不难理解,在验证和推进这些理论的时候,社会学研究者需要关注处理效应的差异。另一方面,从实践的角度出发,大量的以政策分析为导向的研究关注特定人群之间有差异的处理效应(例如:Heckman & Vytlacil,2001;Heckman & García,2017)。这与医学研究中日渐兴起的针对特定类型患者的“精准医疗”存在异曲同工的分析逻辑。显然,这类实践导向的分析要求研究者重视处理效应在不同人群之间呈现出的异质性。
传统的回归模型通过交互项来分析处理效应异质性(Aiken et al.,1991)。之后方法论的发展则日渐依托于倾向值(propensity score)的估算,将处理效应异质性问题转为考察处理效应如何随着个体倾向值的变化而变化(Xie & Wu,2005;Xie et al.,2012;Carneiroet al.,2010;吴晓刚,2008)。这些分析方法虽然展示了处理效应异质性估计的多种策略,但各有其不足之处。随着机器学习方法与社会科学因果推断分析的日渐结合,一个前沿的方法论发展方向是使用基于算法的技术手段来考察处理效应异质性。
在此背景下,本文希望能够通过系统的梳理,展示社会科学研究在考察处理效应异质性时从传统的线性模型到新近的机器学习算法的方法论发展脉络,特别关注不同方法之间的优缺点。在此基础上,本文选取了因果随机森林(causal random forests)和贝叶斯叠加回归树(Bayesian additive regression trees)两个以非参数“树模型”算法为基础的分析技术,具体介绍其算法原理以及如何克服传统处理效应异质性分析的诸多限制。与此同时,本文也反思了以算法为基础的新兴分析技术可能带来的潜在问题,如因参数设定差异和算法差异而损害处理效应异质性分析结果的稳健性。这种分析异质性处理效应时出现的稳健性缺失也可以被称为“异质性的异质性”问题。最后,我们以分析中国精英大学教育回报的异质性模型为例,来展示这些方法论的优势和不足。
二、处理效应异质性的传统分析:方法概观
(一)传统回归模型的交互项分析
对于处理效应异质性的探索,传统的分析手段是在某个回归模型中增加交互项(Aiken et al.,1991)。如果用Y表示因变量,T表示处理变量,C表示某个可能带来处理效应异质性的变量,则交互项模型如模型(1)所示,其中我们关心的系数是β3。

交互项模型虽然使用广泛,但是相关的方法论研究对其是否能够准确呈现处理效应异质性一直有所质疑(Hainmueller et al.,2019)。疑问主要来自两个方面:其一,能够带来处理效应异质性的因素C可能有很多,但是在给定数据的情况下,我们不可能无限制地在模型中添加大量的交互项。因此,对于交互项的设置便具有一定的主观性甚至随意性。其二,交互项的具体形式(变量C的二次方、三次方项,或者三个甚至更多变量交互的情况)往往也是研究者主观设定的,而这种设定并不必然符合数据生成过程的基本特征。交互关系的复杂性通常不会在常规的双变量交互项分析中涉及。
(二)以倾向值为导向的处理效应异质性
当倾向值方法逐渐引入定量社会科学研究以后,对于处理效应异质性的考察便逐渐以倾向值为导向展开(Xie & Wu,2005;Xie et al.,2012)。所谓倾向值,是指个体接受处理变量某个取值水平影响的概率。假设所有的混淆变量(confounding variables)构成矩阵C,那么,倾向值的估计值就是
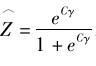
其中γ为矩阵C的系数向量。基于倾向值的此种定义,所谓以倾向值为导向的处理效应异质性分析,就是看处理效应如何随着倾向值取值的变化而发生变化。
以倾向值为导向的处理效应异质性分析有其独特的优点。例如,这条路径不再看某个特定变量C的作用,而是将所有的C降维为一个倾向值Z,进而看倾向值如何异质化处理效应。从这个意义上讲,这一方法克服了上述回归模型交互项的第一个局限。此外,由于处理效应和倾向值构成了一个二维体系,对于它们之间关系的考察也可以突破原有的线性设定,进而采用一些半参数甚至非参数的平滑方法,以应对可能的非线性关系(Keele,2008)。这样,回归模型交互项分析的第二个局限便被克服了。
具体而言,谢宇和其合作者提出了三种以倾向值为导向的处理效应异质性的分析手段(Xie et al.,2012;Zhou & Xie,2020)。一种被称为细分—多层次法(stratification-multilevel method),意指将估算出的倾向值分成不同的取值区间,然后在每个区间内估计处理效应,最后看多个区间的处理效应呈现出何种异质性的变异。第二种方法被称为匹配—平滑法(matching-smoothing method),即先通过倾向值匹配,计算每个匹配对(pair)的处理效应,之后,对于这一系列的基于匹配对的处理效应进行曲线拟合,考察处理效应如何随着倾向值取值的变化而变化。第三种方法被称为平滑—差值法(smoothing-differencing method)。与第二种方法相比,这一方法的特点在于,先分别对实验组和控制组的个体取值Y随着倾向值的变化而变化的模式进行曲线拟合,之后再看两条曲线之间的差值,从而得到处理效应异质性的估计。谢宇等人所提出的这一系列以倾向值为导向的处理效应异质性分析方法和经济学家詹姆士·海克曼提出的边际处理效应(marginal treatment effect)有异曲同工之妙(Carneiro et al.,2010)。关于边际处理效应方法,可参阅胡安宁(2015)、周翔和谢宇(Zhou & Xie,2019)的研究,这里不再赘述。
以倾向值为导向的处理效应异质性分析虽然突破了回归模型交互项的一些局限,但也有自身的问题。首先,倾向值的估计存在着模型不确定性和系数不确定性问题(胡安宁,2017)。其次,将各种混淆因素总结为一个倾向值Z的做法虽然通过降维简化了分析,但是我们也无法具体考察究竟是哪个混淆变量C起到了对处理效应进行异质化的作用。最后,无论谢宇还是海克曼的方法,都重在描述处理效应随着倾向值的取值变化而如何变化,但未能分析是什么因素造成了此种处理效应异质性。
三、以算法为基础的机器学习新工具:因果随机森林与贝叶斯叠加回归树
按照统计学家利欧·布雷曼(Leo Breiman)的经典划分(Breiman,2001),无论是线性回归模型的交互项,还是以倾向值为导向的处理效应异质性分析,都属于以数据随机生成(stochastic generation)为分析基础的模型。这一分析范式需要对统计模型有清晰的设定。与之相应,分析的关注点则放置于模型提供的特定统计量之上(如特定的系数)。与之相比,以算法为基础的分析工具则对数据生成过程存而不论,转而通过在数据上应用特定算法,让数据“说话”,以呈现某种关联性。如果说早期的算法模型因为算力和数据量的限制尚不为社会科学研究者所熟知,那么当我们有足够的计算资源来针对数据使用比较复杂的算法时,我们则不得不正视算法模型在社会科学领域内可能扮演的重要角色。这方面,因果推断技术与机器学习算法的结合正是当下社会科学方法论发展的前沿方向。在已有的一些探索的基础上(例如广义叠加模型[generalized additive modeling]、部分线性模型[partial linear regression]等),涌现了一系列新的适用于因果推断的算法模型。本文针对因果处理效应的异质性,选取了两个以“树模型”算法为基础的分析工具:因果随机森林(Athey et al.,2019;Wager & Athey,2018)和贝叶斯累加回归树(Chipman et al.,2010;Hill et al.,2020)。由于这两个方法都是以树模型为基础展开的,这里首先对树模型进行概览性的介绍。
(一)树模型与随机森林概览
树模型是一系列以数据细分为基础的算法模型的统称(Breiman et al.,1984)。如果分析的因变量Y为分类数据,通常称之为决策树,而如果分析的Y为连续型变量,则称之为回归树。为了表述方便,这里统称为树模型。
一个树模型如图1(a)所示,对于数据中的所有样本,依据某种变量的取值标准,进行不断的细分,从而构建一个树形模型(这里用h指代某一树模型)。例如,我们首先以变量C1为基础,以取值0.5为界,如果大于0.5,则将数据分配分到左边一个树枝,反之则分到右边。在右边这一分支下,依据C2来进行进一步细分,C2大于0.5则到左枝,否则到右枝。究竟在分叉处选取哪个变量以及采用该变量什么数值为界进行细分,都有相应的计算标准(如信息增益比、Gini系数,等等)和算法规则,这里不再赘述。每个树枝的结尾视为一个节点。如果无法进一步细分(例如,节点内的人的Y取值已经比较近似,或者没有足够多的人进行进一步的细分),则每个节点内部所有人Y取值的均值视为符合该节点特征的所有人的Y的估计值。例如,对于C1>0.5的人,估计值为μh1,对于C1<0.5和C2>0.5的人而言,估计值为μh2,最后对于C1<0.5和C2<0.5的人,估计值为μh3。这种对于数据的树状划分等价于图1(a)的右图。
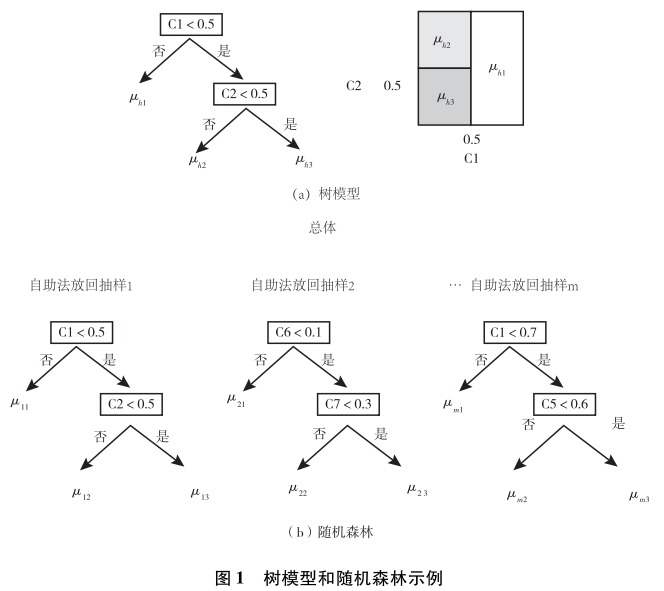
树模型的问题在于这棵树可能会很长,从而带来数据的过度拟合问题。为了解决这一问题,一个常用的技术是随机森林算法,这一算法的逻辑如图1(b)所示。随机森林涉及两个随机。一个随机是从分析对象总体中采用自助法(bootstrap)抽样得到多个子样本(假设共M个子样本),之后在每个子样本中拟合树模型。另一个随机是在每个树模型的分叉点,采用的分叉变量是从所有的备选变量中随机选取产生的。例如,在图1(b)中,第一个树模型用到的变量是C1和C2,第二个树模型用的是C6和C7,第m个树模型用的变量是C1和C5。在得到M个树模型之后,对于某个个体,基于其一系列的背景特征,我们可以得到M个对于其Y值的估计值。假设某个个体的取值为C1=0.6,C2=0.2,C5=0.3,C6=0.8,C7=0.2,则在第一棵树下,其Y的估计值为μ11,第二棵树下的估计值是μ21,第m棵树下的估计值是μm3。如果Y是一个连续型变量,我们就可以计算这m个估计值的平均值,从而得到对于Y的整体估计
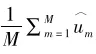
如果Y是一个分类变量,那么我们可以采用投票的方式(例如服从多数原则)决定Y的整体估计值。
(二)因果随机森林
因果随机森林可以看作是随机森林算法在因果推断问题上的直接应用(Athey et al.,2019;Wager & Athey,2018)。这一方法的基本目的是最大化处理效应在不同树模型节点之间的变异。具体而言,因果随机森林和传统随机森林方法相比,在节点分叉、模型拟合和处理效应估计三个方面都有自己的特点。
节点分叉。我们用P表示母节点,其分叉为左右两个子节点C1和C2。那么,在传统的树模型中,我们判断是否继续分叉的依据可以是分叉后每个子节点内部对Y的估计误差。例如,假设两个子节点C1和C2对Y的估计值分别为μ^c1和μ^c2,其样本量分别为nC1和nC2,处于两个子节点中分析对象Y的观测值分别表示为YC1和YC2,则两个子节点的估计误差分别为
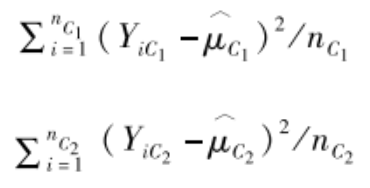
那么,如果C1和C2中个体人数比例分别为
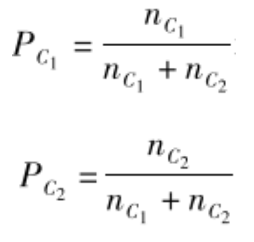
那么节点分叉后的总误差为:
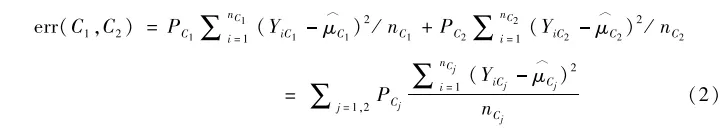
从方差分析的角度来看,上面的分叉标准实际上是要求组内方差最小化。与之相比,因果随机森林则在每个节点内估计因果效果τ^c1和τ^c2(如每个节点内部实验组的Y的均值减去控制组的Y的均值。当然,这里需要保证每个节点内部有实验组和控制组的个体,详见下面的参数设置)。此时在决定节点是否继续分叉时,所采用的标准就不再基于节点内部方差最小,而是节点间变异最大,即希望以节点之间因果效果的彼此差异最大化。顺着这一思路,因果随机森林的节点分叉标准变成了最小化下面的误差表达式:

其中,E(τ^Cj)表示不同节点处理效应的期望值。对于这一误差表达式,经济学家苏珊·阿西(Susan Athey)等人证明
errcausal(C1,C2)=常数项-+随机扰动项。
所以,我们最小化errcausal(C1,C2)等价于最大化

即节点之间估计的处理效应彼此差异尽可能大。显然,这实际上就是处理效应的异质性。
模型拟合。和传统随机森林相比,因果随机森林在模型拟合方面可以选择所谓的诚实(honesty)算法。在传统随机森林算法中,数据分为训练组(training)和测试组(testing),其中训练组用来建立一系列的树模型和估算节点中Y的估计值û,而测试组则是用新的数据来对模型进行应用(如计算新来人员的û)。但是在因果随机森林中,诚实算法要求构建树模型和估计τ^分开进行。也就是说,训练组数据进而分为两部分,一部分用于构建树模型(仍旧称为训练组),一部分用于计算节点内部的处理效应τ^(可以被称为估计组)。这样做的好处在于减少τ^的估计误差。在实际操作中,研究人员可以自行选择是否采用诚实算法。这是因为尽管诚实算法有其优势,但是在使用的过程中,训练组数据要分割使用,因此会压缩树模型的训练数据集。
处理效应估计。基于一系列的树模型(或者森林),最后一步是对处理效应进行估计。如果有新的观测对象(即没有用于树模型拟合和û估计的新的数据),基于其背景特征C,我们可以用因果随机森林来估计某一处理变量对于这一观测对象的Y的处理效应。具体而言,对于这个新的分析对象i,我们可以根据因果随机森林中一系列的树模型计算训练组中的所有数据点和i同分到一个节点的频数。频数越高的人(如个体j)和个体i的背景越接近,自然我们就应当在计算针对i的处理效应的时候给j更大的权重。如果没有新的测试数据,可以采用包外(out-of-bag)估计来计算权重。
(三)贝叶斯叠加回归树
与因果随机森林相比,贝叶斯叠加回归树虽然也是基于树模型算法的分析技术,但在对树模型的使用上有其独特之处(参见Chipman et al.,2010;关于该方法的系统梳理,参见Hill et al.,2020)。为了理解贝叶斯叠加回归树,我们首先来看什么是叠加回归树。顾名思义,叠加回归树将Y的预测值写成多个树模型的叠加。如上文所示,一个树模型涉及输入信息X(处理变量和各种混淆变量构成的矩阵,即X是由T和C构成的矩阵,X=[T,C]),建构的树Tree,以及节点输出μ。为了表述的方便,我们可以用函数g来将三者结合起来,写为g(X,Treeh,Mh),其中下标h表示第h个树模型。基于这些信息,我们可以把Y的估计值Y^写成如下叠加回归树的形式:
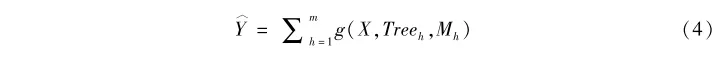
其中,一共有M个树模型,每个树模型用Treeh表示,而Mh=(μh1,μh2,…,μhI)’指代每个树模型的节点处对于Y的预测值。基于这种设定,我们可以把观测值Y写成叠加模型的形式。假设ε是服从均值为0、方差为σ2的随机扰动项,我们有:
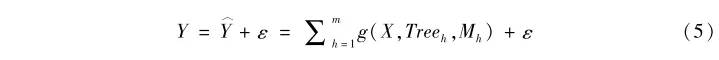
至此,我们建构了一个叠加模型。而贝叶斯叠加回归树提供了针对它的估计方法。这个方法的优点在于通过调控各种参数先验分布的特征来控制潜在的过拟合。实际上,叠加树模型非常容易出现过拟合。例如,先拟合树模型Tree1,之后计算Y减去Tree1得到残差e1,然后再对e1拟合Tree2,然后计算扣除Tree2后的残差e2,并针对e2拟合Tree3,依次类推。可见,只要树模型的数量足够多,结构足够复杂,必然会对数据过拟合。而引入贝叶斯的先验概率则有效地控制了这种过拟合情况。
具体而言,在上述模型中一共有三个参数:Treeh,Mh和σ2。贝叶斯叠加回归树通过分别对它们设定先验概率保证每个g(x,Treeh,Mh)都是一个弱学习器。正是因为如此,这些先验概率也被称为正则(regularization)先验。具体而言,贝叶斯叠加回归树设定σ2服从反伽马分布,这一分布的均值设为Y的观测数据的标准差σ^。但是这个参数需要进行一定的数学变换以保证P(σ<σ^)=0.95。每个树模型Treeh的先验分布设置为α(1+d)-β,其中α取值在0到1之间,β>0,d表示的是一个树模型的树深度(depth),即从顶点到最下面一个节点经过多少分叉。通常我们取α=0.95,β=2,由于-β是一个负值,这一先验分布使得结构非常复杂的树模型出现的概率很小。即树模型越复杂,出现概率越小。对于Mh,贝叶斯叠加回归树设定节点的一系列对Y的估计值服从正态分布。假设某个树模型下有t个节点,则设定μht服从均值为0、方差为ω2的正态分布。对于这一正态分布,设定ω=0.5/k√M。其中k可以取值为2,M为树模型的数量。可见,树模型越多,ω2越小,μht的分布越集中于均值0。也就是说,很多μht的取值会被强制接近于0,从而控制了单个树模型的影响力,抑制过拟合。最后,和一般的树模型一样,树模型分叉处选用的变量和其取值界限的选择均设定为均匀分布。
在完成上述先验分布的设定后,贝叶斯叠加回归树的估计就进入到传统的马尔科夫链-蒙特卡洛计算过程,以模拟后验分布。具体的技术细节这里不再赘述,具体参见戈尔曼等人的著作(Gelman et al.,2013)。基于后验分布,我们可以通过改变自变量T的取值,模拟T在不同取值下Y的变化,以此估计出处理效应。例如,对于个体A,假设其X取值为[1,C]。那么,个体A在T=1时的Y的观测值Yobs即为其在实验组时的Y值,我们可以利用贝叶斯叠加回归树来模拟当个体A的T取值为0的时候Y的估计值。例如,我们可以把个体A的T值强制赋值为0,并将其作为一个新的观测样本放入贝叶斯叠加回归树(X设置为[0,C]),得到的预测值Y^即为当个体A在控制组时的Y的估计。那么,对于个体A而言,其处理效应为Yobs-Y^。
(四)树模型的可解释性:变量的重要性指标
对于定量社会科学经验研究而言,学者们非常重视模型的“可解释性”。在因果推断研究中,处理变量和因变量的定义非常明确。因此,模型的可解释性往往落脚点在如何理解控制变量(或者称为混淆变量)在估算因果关系过程中的作用(Molnar,2020)。对于树模型而言,由于在每个树分叉节点处需要对各个混淆变量逐一“扫描”,那么多个树节点下,有的混淆变量就会被使用很多次,而有的混淆变量被使用的次数更少。这种使用次数的差异本质上代表了某一个混淆变量对于某一因变量的“解释”能力。解释能力越高,被用来进行节点分割的次数就会越多。那么我们就可以看多个树模型下,哪些混淆变量更受“重用”,从而了解不同的混淆变量跨越多个树模型的整体“重要性”程度。在机器学习文献中,这种混淆因素的重要性也被称为特征重要性(feature importance)。
这里需要指出的是,混淆变量的特征重要性,在因果随机森林和贝叶斯叠加回归树这两个模型之间有不同的含义:贝叶斯叠加回归树进行的是传统的树模型拟合,混淆变量的作用在于在每一个节点处提升因变量Y在子节点内的“纯度”,而因果随机森林则要求每个节点处选取的混淆变量可以提高子节点彼此之间因果效应估计上的差异。换句话说,贝叶斯叠加回归树中重要的混淆变量是那些能够最大化区分因变量取值的变量,因果随机森林中重要的混淆变量是那些能够区分处理效应的变量。这种特征重要性定义上的差异需要特别注意。
四、新工具、新机遇、新挑战
与传统回归交互项和以倾向值为基础的处理效应异质性分析不同,无论是因果随机森林还是贝叶斯叠加回归树,都是基于更为复杂的树模型算法对数据进行处理的。这两种方法为我们提供了估计处理效应异质性的新工具。基于其方法特点,它们为定量社会科学研究者提供了新的机遇,也带来新的挑战。
(一)新机遇:个体处理效应的趋近及其应用
与传统的方法相比,因果随机森林和贝叶斯叠加回归树的一个优势在于,可以为我们提供对个体处理效应的趋近(approximation)估计。众所周知,因果推论过程中的一个基本问题是我们无法同时观测到一个个体的观测值与反事实(counterfactual)值(Holland,1986)。也正是由于这一点,常规的因果推断技术往往估计的是特定群体的“平均”处理效应,而不是个体处理效应。
虽然反事实状态难以直接观测,但我们可以将其看成是一个缺失值并填充之(Ding & Li,2018)。换句话说,我们只需要通过某种手段把反事实状态这一缺失值填补进去,然后与观测到的事实状态相减就能够获知个体处理效应的一个估计。顺着缺失值填充的思路,现有文献提供了两种策略。一种策略是“匹配”,即尽可能寻找那些与被研究个体接近、但是T取值不同的分析对象来进行匹配(Stuart,2010)。另一种策略是“模拟”(Abadie & Imbens,2011)。其思路是尽可能地拟合一个完备的针对因变量Y的模型。通过这个模型,我们可以知道,究竟是哪些因素能够影响Y以及如何影响。个体A只要服从这个模型,那么只需要改变个体A的T取值,就能够近似地估算出个体A的反事实状态。换句话说,T取值不同时Y的取值差异可以用来趋近个体处理效应。
通过上面的方法论介绍不难发现,因果随机森林采取了“匹配”的策略。通过生成不同的树模型,训练组中的每个个体都获得了一个权重,代表了在各个树模型中与我们关心的个体出现在同一个树节点内的概率。由于划分到同一个节点的个体在大量的混淆变量C上取值相同,因此这一权重本质上反映了训练组中的个体与我们关心的个体的接近程度,或者说匹配度。权重越大,与我们关心的对象越相像,就越能够影响个体处理效应的估计。与之相比,贝叶斯叠加回归树则采取了“模拟”的策略。通过贝叶斯方法,我们基于先验分布的参数值设置可以获取一系列参数的后验分布,即叠加回归树的基本分布状态。那么,我们如果想估计个体A的个体处理效应,只需要将个体A的信息代入,让叠加回归树估算个体A的T在取值不同时的Y的期望值并相减之,由此就得到了个体A的个体处理效应估计。其分析过程的依据在于存在一个训练得很好的叠加树模型,以供我们“模拟”出反事实的取值。
那么,利用因果随机森林和贝叶斯叠加回归树来趋近个体处理效应,对于处理效应异质性的分析有何价值呢?首先,因果随机森林和贝叶斯叠加回归树都是基于算法建构树模型的。因此,这两个方法尽可能地避免了对于模型形式的人为设定和干扰。这就在一定程度上突破了回归模型交互项以及以倾向值为导向的处理效应异质性考察在模型形式上的限制。其次,树模型的建构过程(如设置分叉点)不断地对混淆变量取值的组合进行考察(T除外),因此,因果随机森林和贝叶斯叠加回归树的一个特点在于几乎可以穷尽处理变量T和各种其他混淆变量之间的交互关系。这种对于交互关系的穷尽是传统处理效应异质性分析方法无法完成的。最后,个体处理效应的估计值可以成为进一步分析的对象。如上文所述,传统的回归模型交互项和以倾向值为导向的分析重在展示而非解释异质性。与之相比,因果随机森林和贝叶斯叠加回归树帮助研究者估计某个处理变量在“每个人”身上的处理效应大小。那么,我们自然可以进一步看,究竟是什么因素影响了这种个体间的差异,从而“解释”了处理效应异质性。
(二)新挑战:异质性的异质性
虽然因果随机森林和贝叶斯叠加回归树通过趋近个体处理效应为我们考察处理效应异质性提供了新的思路,但这两种方法也给经验研究者带来了新的挑战。这个挑战我们称为“异质性的异质性”(heterogeneity of heterogeneity):前一个“异质性”是指对处理效应异质性的估计,后一个“异质性”指的是这种估计会因为算法出现经验结果彼此不一致的情况。
具体而言,造成异质性的异质性现象的原因有二。一方面,与传统的统计分析相比,基于算法的分析手段需要对更多的算法参数进行设定。虽然基本上大多数的算法模型都提供了默认值,但是此种默认值并非基于具体问题设定,因此无法保证普适性。在这种情况下,不同的研究者可能会有不同的参数设定偏好。其结果便是,即使分析同样的问题,也有可能因为算法参数设定不同而出现分析结果的差异性。另一方面,分析结果还有可能因为算法本身的不同而出现差异。在以机器学习为基础的各种分析技术中,相较于传统模型,算法被推到一个非常重要的地位。在非学术研究的商业应用中,甚至有算法霸权一说(奥尼尔,2018)。尽管目前在社会科学领域内谈算法霸权似乎为时过早,但是算法无疑是决定经验结果的一个重要因素,而不同算法的差异则有可能成为造成经验结果异质性的重要原因。
五、经验示例
(一)研究问题与数据
本文的经验示例分析了中国精英大学教育回报的异质性,即与一般大学相比,进入精英大学学习的收入回报在不同个体之间是否以及如何呈现出异质性特征(Hu & Vargas,2015)。数据来自于“首都大学生成长追踪调查”(Beijing College Students Panel Survey,BCSPS)。这一数据提供了大量学生进入大学之前的背景信息,这些信息构成了研究中的潜在混淆变量,从而有助于抑制潜在的选择性误差。此外,由于是追踪数据,我们在后续调查中获取了大学生毕业后的初职收入信息。在下面的分析中,精英大学选取的是北大、清华和中国人民大学三所大学,这三所大学构成了BCSPS调查三个独立的抽样框,因此保证了足够的样本量。首都大学生成长追踪调查的相关信息可以参阅吴晓刚(2016)。
(二)变量选择
下面分析的处理变量为是否毕业于清华、北大或者人大(1=是,0=否),因变量则是初职月收入水平。除了这两个变量之外,我们还考虑了其他潜在的混淆变量,包括性别(1=女,0=男),民族(1=汉,0=少数民族),年龄,是否高中复读(1=是,0=否),目前所在年级(1=大学一年级,3=大学三年级),家庭年收入(log转换),兄弟姐妹数量,父亲教育水平(1=未受过正式教育,2=小学,3=初中,4=高中,5=职高/技校,6=中专,7=大专,8=本科,9=研究生及以上),母亲教育水平(1=未受过正式教育,2=小学,3=初中,4=高中,5=职高/技校,6=中专,7=大专,8=本科,9=研究生及以上),父亲是否党员(1=是,0=否),母亲是否党员(1=是,0=否),父亲是否全职工作(1=是,0=否),母亲是否全职工作(1=是,0=否),高中中学等级(1=全国重点中学,2=省重点中学,3=地市重点中学,4=县重点中学,5=非重点中学)以及入学前的所在地区(1=东部省份,2=中部省份,3=西部省份)。
(三)传统分析方法的结果
如上文所述,我们研究与一般大学相比,精英大学对于收入的影响异质性。我们首先看精英大学的收入回报异质性是否和进入精英大学的概率(倾向值)相关(Brand & Xie,2010)。在表1中,模型I利用一系列的背景变量拟合了logistic回归模型。基于此模型,我们进一步估计每个分析对象的倾向值。模型II建立了最小二乘回归(OLS)模型,并考虑处理变量和倾向值的交互关系。结果表明,精英大学的收入回报与倾向值的交互并不显著。因此,仅就回归模型交互项来看,不存在处理效应随着倾向值变化而变化的情况。
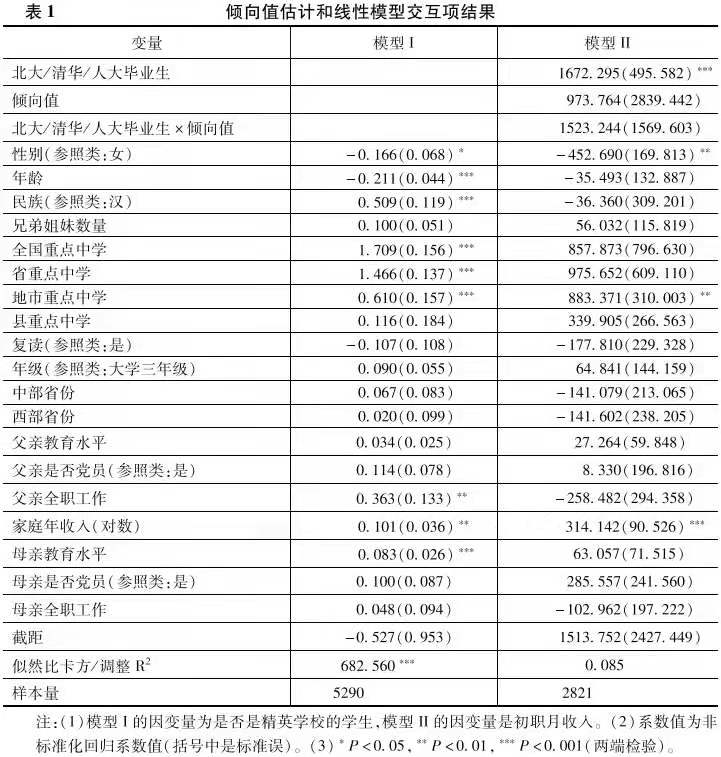
图2展示了谢宇等人的三个处理效应异质性分析方法以及海克曼的边际处理效应模型的结果。细分—多层次法说明存在明显的正向选择效应,即越容易进入精英大学的人,其教育回报越高(斜向上的趋势)。但是,如果看匹配—平滑法和平滑—差值法的分析结果,则没有明显的异质性处理效应。最后,边际处理效应的结果也支持了正向选择效应的结论(横轴是阻碍变量,其与倾向值含义相反)。
综上所述,回归模型的交互项、匹配—平滑法和平滑—差值法的分析结果都没有提供证据来支持处理效应的异质性,但是细分—多层次法和边际处理效应分析都显示出一定的处理效应异质性。这种差异本身体现了不同的分析方法对于分析结论的影响。那么,如果基于个体处理效应的趋近,我们能够得出什么结论呢?下面我们就分别采用因果随机森林和贝叶斯叠加回归树进行分析。
(四)个体处理效应的趋近及其使用
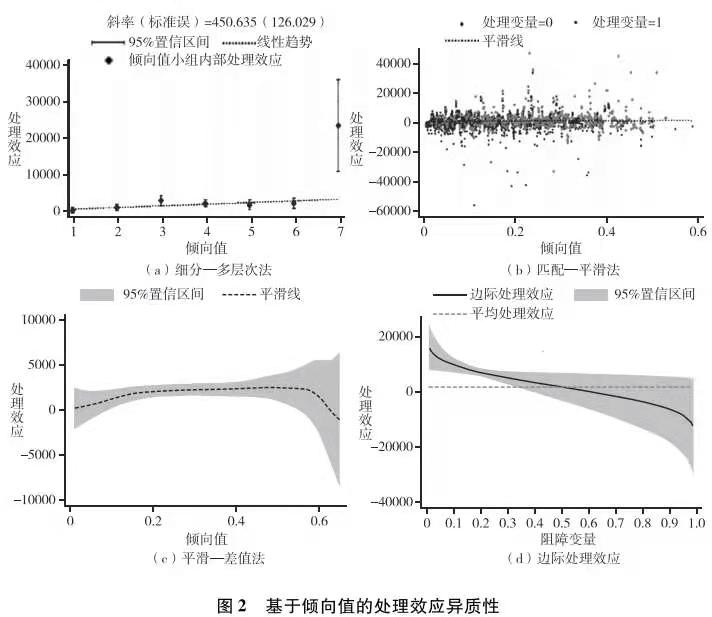
利用因果随机森林和贝叶斯叠加回归树可以估计出个体处理效应。我们这里采用核密度分布勾勒其基本分布状态。我们的带宽为115,核函数用的是常见的叶帕涅奇尼科夫(Epanechnikov)核函数。以某一观测值为中心,这个核函数规定了权重在左右两边呈抛物线状下降,并服从公式0.75×(1-x)2。对于我们分析的样本,两种方法得到的处理效应的核密度分布如图3所示。
图3呈现三个特征。其一,两个分布基本上重叠,且形状近似,这说明通过因果随机森林与贝叶斯叠加回归树估计出的个体层次上的因果效果具有比较高的一致性。其二,两个分布的最高点彼此不同。落实到X轴上,可以看到贝叶斯叠加回归树的“众值点”(分布峰部对应的X轴取值)大于因果随机森林的“众值点”。因此,二者的估计在最有可能出现的因果效应值上有所不同。第三,两个分布显示出比较明显的数据离散度。这说明,同样是考察精英大学的收入回报,处理效应在人和人之间存在很强的异质性。
那么,为了得到这些估计,哪些混淆因素比较重要呢?为了回答这一问题,我们展示了混淆变量的特征重要性指标,如图4所示。
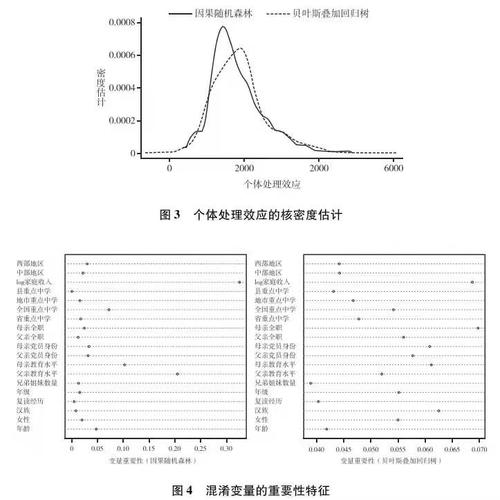
在两种方法中,家庭收入均是一个关键的混淆变量。但是对于因果随机森林而言,次重要的混淆因素是父母的教育水平,但是在贝叶斯叠加回归树中,次重要的混淆因素是母亲是否全职和是否为汉族。如上文所述,混淆变量的重要性在两种方法之间存在定义上的差别,因此这种经验结果上的差异可以理解。需要指出的是,我们也计算了两种方法下混淆变量重要性排序的斯皮尔曼排序相关系数(ρ),结果发现,在两种方法下不同混淆变量的排序具有较高的相关性(ρ=0.36;P=0.137)。这说明,尽管在不同方法下混淆变量重要性指标的定义有所不同,但整体而言,各个混淆变量的重要性顺序具有较高的一致性。
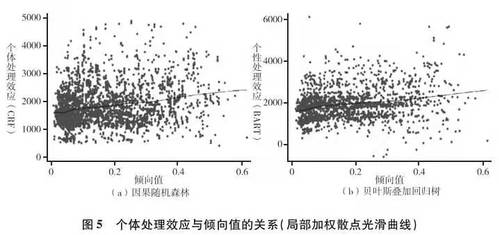
基于个体层次的处理效应估计,我们可以直接用散点图来观察处理效应如何随着倾向值的变化而变化。相关的结果参见图5。无论采用哪种分析方法,其估计出的个体处理效应都和倾向值之间存在正向的联系(P<0.001)。即,精英大学的回报随着进入精英大学概率的增大而增大,即存在某种正向选择效应。
下面,我们可以进一步探索哪些具体的混淆变量能够影响处理效应异质性。OLS模型的分析结果参见表2。其中,兄弟姐妹数量、父亲教育水平和家庭收入的提升可以显著提升个体处理效应。这在一定程度上说明,出身良好家庭背景的个体进入精英大学,其从大学教育经历中获得的回报相比于出身一般家庭背景的个体更高。但是来自全国重点中学的精英大学学生的回报反而偏低,这或许与样本选择效应有关(例如,全国重点中学的学生有相当一部分高中毕业后选择出国而非留在国内读书,或者他们在国内精英大学毕业后更倾向于继续深造而不是立刻工作。此时,立刻进入劳动力市场的精英大学毕业生或许并不是那些最能够从劳动力市场获取高收入的群体)。除了这些变量,母亲教育水平和全职工作虽然在两个模型中都是显著的,但是估计的效应相反。
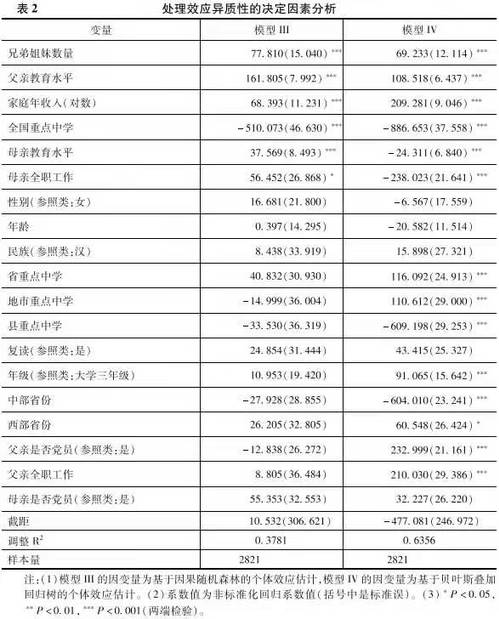
上面的分析结果显示了两种分析方法彼此之间的差异。例如,对于个体层次的因果处理效应估计,基于贝叶斯叠加回归树的分析结果表明,诸如学校等级、年级、省份、父亲是否党员以及工作状态这些混淆变量都有显著的相关性。但是基于因果随机森林的分析结果没有展示出类似的经验模式。这种差异或是不同的算法逻辑所致,关于这一点,下文对于“异质性的异质性”的分析将进行讨论。除此之外,另外一个可能性在于数据量的限制。基于算法的分析技术往往需要“海量数据”的支撑,以便有足够的信息进行模型的训练。因此,本文2821的数据量对于训练因果随机森林和贝叶斯叠加回归树而言或许不够。如果是这样的话,那么训练出的模型有可能不够精确,从而带来了因果随机森林与贝叶斯叠加回归树之间的差异。我们这里借助自助法(bootstrap)的思路来检验一下数据量大小的潜在影响。具体而言,我们采用放回抽样的方式,以原始的首都大学生成长追踪调查数据为基础,生成了一个10万样本量的新数据。分析发现,即使我们把样本扩充到10万,不同的方法所估计出的个体层次处理效应与混淆变量的关系依旧呈现明显的方法间差异。基于这一发现,我们可以初步认为,上面呈现的经验结果差异应当主要归因于不同方法之间的差异,而不是样本量问题。
(五)异质性的异质性
在展示了以机器学习算法为基础的方法优势之后,本部分将着重展示“异质性的异质性”对研究者提出的新挑战。我们首先考察内部的异质性,通过调整算法基本参数,看经验分析结果的变异度(上面的分析基于参数的默认取值)。针对因果随机森林,我们先后拟合基本模型(各种参数设为默认值)、变量选择模型(基于随机森林的变量重要性指标,仅保留重要性大于所有变量重要性均值的变量)、诚实算法模型(采用诚实算法如果采用诚实算法,那么我们在训练数据中再将其中50%用于树的分叉设置,50%用于填充数据。即在所有样本中,25%(即50%×50%)用于分叉,25%用于数据填充。)和不同样本比例模型。样本比例是指在总样本中用于训练树模型的训练组样本所占的比例,这里先后设置为30%、20%和10%。这样,对于因果随机森林,我们一共有六个基于不同算法参数的模型,其个体处理效应的估计分布及其相互关系如图6所示。
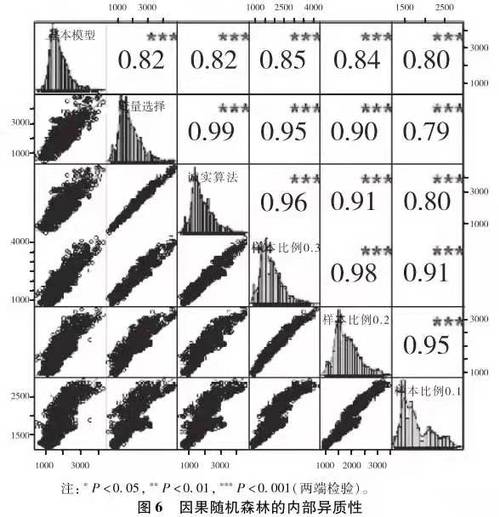
通过图6可以发现,尽管不同的模型参数设定下的个体处理效应分布有些许差异,但整体而言,不同的参数所估计出的结果之间有着比较高的相关性(相关系数如右上角的数字显示,取值区间为0.79-0.98,且均统计显著)。因此,因果随机森林呈现比较低的内部异质性。
如上述讨论,贝叶斯叠加回归树的主要的参数是树模型的数量。其中默认的是200。除了这一基本模型外,我们先后拟合了5个、10个、50个、100个和500个回归树的贝叶斯叠加回归树模型。其对于个体处理效应的估计及其相互关系如图7所示。
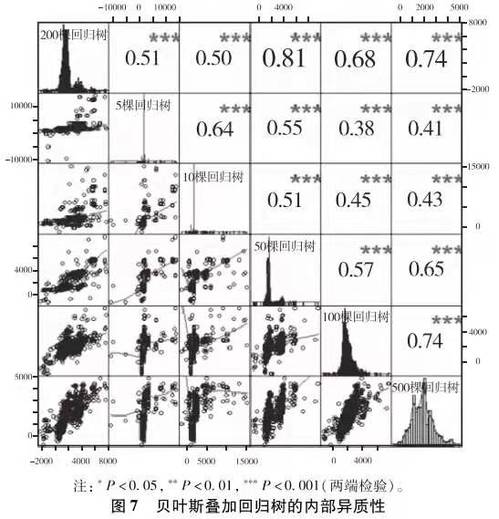
显然,贝叶斯叠加回归树的内部异质性程度很高,尽管相关系数都统计显著,不同的参数设定估计出的个体处理效应上相关性并不是很强。
外部异质性可以通过对比因果随机森林与贝叶斯叠加回归树的分析结果来进行考察。我们这里看个体处理效应估计值的相关性。如果外部异质性低,则两种算法估算出的个体处理效应应该彼此接近,从而具有较高的相关性,否则,我们有理由认为存在比较高的外部异质性。分析结果参见图8。图中被方框圈出来的是两种算法下个体处理效应估计的相关系数矩阵。显然,其相关性不是很高。这表明不同的算法之间呈现的分析结果具有较强的外部异质性。

综上所述,因果随机森林具有比较低的内部异质性,而贝叶斯叠加回归树则具有比较高的内部异质性。两种算法的结果相对比,说明基于算法的分析手段具有比较高的外部异质性。
六、结语
社会科学经验研究估计的处理效应因为个体间的差异而存在异质性。传统上对于处理效应异质性的分析依赖回归模型交互项。但是这一方法存在变量选择和模型形式等限制,这些限制促使研究者转而考察处理效应如何随着倾向值取值改变而呈现出变异性。这种以倾向值为导向的处理效应异质性分析克服了传统回归模型交互项的限制,但是引入倾向值的估计方程会带来模型和估计的不确定性。此外,以倾向值为导向展开的处理效应异质性分析因为倾向值对混淆变量的“总结”而无法直接分析哪个变量带来了异质化的效果。最后,这一方法重在展示异质性,而较少考虑是什么因素造成了此种异质性。在此背景下,以算法为基础的各种机器学习方法应运而生。以因果随机森林与贝叶斯叠加回归树为例,这些新兴分析手段因为无模型预设,从而克服了参数设定上的限制。此外,两种方法充分考虑了处理变量同其他各种混淆变量的交互关系。因果随机森林与贝叶斯叠加回归树亦分别体现了“匹配”和“模拟”的分析逻辑,以估计和趋近个体处理效应,从而能够帮助研究者分析处理效应异质性的决定因素,同时呈现出处理效应异质性的经验分布。然而,新的分析手段也为经验研究者带来了新的问题,如因为参数设定不同而带来的内部异质性以及因为算法不同而带来的外部异质性。
随着算力的提升和相关统计分析软件的普及,以算法为基础的机器学习方法和定量社会科学研究的结合已然成为可能。这一方法论发展对于社会学本身的影响值得反思与讨论。与传统的社会学量化分析手段(如回归模型等)相比,机器学习技术以算法为核心,无论是模型建构逻辑(以理解数据生成过程为目的或以预测为目的),还是具体操作(使用封装好的程序还是研究者人为设定多种参数),机器学习技术都有其独特之处。因此,机器学习技术可以视作常规量化分析手段之外,经验社会学者的新的工具。这种新工具既可以独立使用,也可以用于发展传统的分析方法(例如突破模型形式的建模等),因此值得社会学经验研究者予以特别重视。当然,对于社会学学科本身而言,这也意味着传统量化方法培养内容的更新与改变。此外,考虑到机器学习方法在社会学之外各个领域内的广泛运用(例如商业分析、城市规划分析等),将机器学习引入社会学也不失为一种推进跨学科合作交流的手段。
本研究围绕机器学习与因果推论的结合进行了一系列的讨论,但以算法为导向的分析手段仅仅是计算社会科学时代下的一个发展方向。除了在分析工具上引入算法模型之外,计算社会科学兴起的一个重要标志是对大量非结构性数据的分析以及对于复杂模型某一模式涌现的考察。这些新的发展方向如何共同形塑量化社会科学的学科特点和未来,值得加以深入地探讨。
【作者简介】

胡安宁,复旦大学社会发展与公共政策学院教授、博士生导师。国家以及上海市多个人才称号获得者。主要从事文化社会学、教育社会学、社会不平等、社会科学量化研究方法研究。先后在《中国社会科学》、《社会学研究》、《社会》以及 British Journal of Sociology, Social Science Research, Journal of Marriage and Family,Poetics等国内外知名期刊发表论文 70 余篇,出版专著多部。
